BQ #6: Unit U Concepts 1-8

1- What is a continuity? What is a discontinuity?
 A continuity is when the function is predictable, has no breaks, holes, or jumps, and can be drawn without lifting your pencil. A discontinuity is when the function DOES have holes, breaks, or jumps, and it isn't predictable. As well does a discontinuity have two types of families:
The first type of family is the Removable Discontinuities- This family only has the Point Discontinuity, which is pretty much a graphed out line with a hole in it (it can also be a hole with a point above it).
 Ex.

http://bfreshrize.files.wordpress.com/2012/01/unknown.jpeg?w=500

The second type of family is the Non-Removable Discontinuities- This family has three discontinuities. The first one is the Jump Discontinuity, which is similar to piecewise graphs however both parts cannot have closed points but can have them both open or one open and one closed.
Ex.

http://image.tutorvista.com/content/feed/u364/discontin.GIF

The second one is Oscillating Behavior, which is just a line graphed out that is extremely "wiggly" that it makes it almost impossible to find the height, limit, and value of it.
Ex.

http://webpages.charter.net/mwhitneyshhs/calculus/limits/limit-graph8.jpg

The last one is the Infinite Discontinuity, which is also known as unbounded behavior and it occurs were there is a vertical asymptote.
Ex.

http://www.math.brown.edu/utra/discontinuities%201.GIF

2- What is a limit? When does a limit exist? What is the difference between a limit and a value?
 A limit is the intended height of a function. The limit exists whenever you reach the same height from both the left and right (on a continuity). However it does not exist when you cannot reach the same height from both the left and right (on a discontinuity). The difference between the two is that a limit is the intended height while the value is the actual height of the function.
3- How do we evaluate limits numerically, graphically, and algebraically?
When evaluating limits numerically you just have to create a table to find the points closest to the value and vise versa to find the limit.
Ex.

http://media.showme.com/files/349881/pictures/thumbs/658760/last_thumb1359484583_200x150.jpg

To find limits graphically, we use our fingertips and follow the line to the point that we are looking for.
Ex.

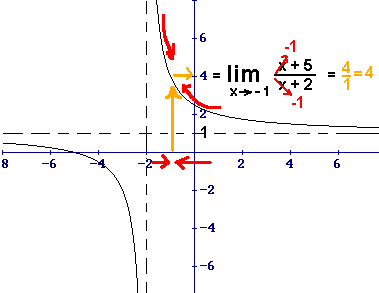http://www.mathnstuff.com/math/spoken/here/2class/420/c42d.gif

When finding limits algebraically, we use three methods: Direct Substitution, Dividing out/Factoring, or Rationalizing/Conjugate. However when finding limits algebraically we must always start with direct substitution to make sure that it equals 0/0 for we can do anymore, for if it equaled a real number to begin with all of the work done would have wasted time.
Ex. (Substitution)

Ex. (Factoring)

Ex. (Rationalizing)

BQ #3: Unit T Concepts 1-3

1-How do the graphs of sine and cosine relate to each of the others? Emphasize asymptotes in your response.
A: Tangent?

B: Cotangent?

C: Secant?

D: Cosecant?

BQ #4: Unit t Concept 3

1-Why is a "normal" tangent graph uphill, but a "normal cotangent graph downhill? Use the Unit Circle Ratios to explain.
The reason why is because there is a difference in the asymptotes. The asymptotes are shifted in different places because of the fact that tangent and cotangent are reciprocals, for example tan=y/x therefore making the focus be on "x" because when finding the asymptote "x" must equal zero and so the only areas that are equal to zero is at 90 and 270 degrees. While for cotangent, cot=x/y so the "y" id now the one that has to be equal to zero and that is at 0, 180, and 360 degrees, with that there is a shift from where the asymptotes will be at. Making tangent go uphill and cotangent go downhill. If you are still confused look at the picture at the bottom.

BQ #5: Unit T Concepts 1-3

1-Why do sine and cosine NOT have asymptotes, but the other four trig functions do? Use Unit Cirlce ratios to explain.
The reason why sine and cosine do not have asymptotes is because their trig ratios (sin=y/r and cos=x/r) and always on top of 1 ("r") making them to never be undefined. While the other four trig functions (csc=r/y, sec=r/x, tan=y/x, and cot=x/y) are not over 1 and therefore their denominator can equal 0 which will equal to be undefined and will create the asymptotes.

BQ #2: Unit T Intro

1-How do the trig graphs relate to the Unit Circle?
A) Period?-Why is the period for sine and cosine 2 pi, whereas the period for tangent and cotangent is pi?
The reason why the period for sine and cosine is 2 pi is because in the unit circle it takes them the whole 360 degrees in order to repeat it's pattern. For example for sine in the first and second quadrants it is positive but in the third and fourth quadrants it is negative so in order to see the pattern repeat one must wait until another 2 pi goes around. While for tangent it only takes pi because in the unit circle it is positive in the first quadrant and negative in the second allowing the pattern to repeat itself again in the next two quadrants. If unclear (for visual) look at the picture below.

B) Amplitude?-How does the fact of that sine and cosine have amplitudes of one relate to what we know about the Unit Circle?
Sine and cosine equaling to one is related to the unit circle because they both can be between 1 and -1 because of their trig functions we used in the Unit Circle before (sin=y/r and cos=x/r). While the other functions don't have amplitudes because of the fact that they don't have restriction. For example, tan=y/x because of this tan can be equal to anything that can be inside and outside the Unit Circle.

Reflection #1: Unit Q: Verifying Trig Identities

1- What does it actually mean to verify a trig identity?
To verify a trig function actually means to solve a very "complicated" equation with trig functions in them. the reason in why i say that they are "complicated" is because in all reality when you know how to do them, the problem will already give you an answer and you just have to see if it is true or you are to just simplify it to the best of your abilities.

2- What tricks and tips have you found helpful?
I found the tip of doing the hardest side first to be very helpful because when I finished the hardest I knew that I was able to solve the rest of the equation fairly quick because I already did the most challenging part of the whole equation. As well was the trick of memorizing the trig identities helped me a lot, yes it was a pain to memorize more equations however in the long run it helped me so much especially during the test because I was able to name identities and was able to cut the work load almost in half. As well as being to split fractions into two monomial denominators because it helped me a lot when I got stuck in solving equations that I thought might have not even had an answer.

3- Explain your thought process and steps you take in verifying a trig identity
Well my first step in doing this is to see whether there is an identity that I can switch for one of the Pythagorean theorems, but if there isn't any then I convert everything to sine and cosine. What I then do is try to cross cancel or I keep looking if there are more Pythagorean theorems. If not and they are in a fraction, then I split them into two monomial denominators or I use their reciprocals to cancel out and find Pythagorean theorems (I only use this when I feel like I am stuck on the problem).

SP #7: Unit Q Concept 2- Find all trig functions given one trig function and a quadrant

In this concept we see how we can find all trig functions when given just one trig function and a quadrant. You can find this very easily with SOHCAHTOA or just use this method to check your work. This is the problem of my partner, Genesis R., and mine. Please try to answer it before looking at the answers below:
Tanx= -8/5, Cosx= 5rad89/89

However this isn't the only way to find these answers if you want to learn how to get the same result but with Identities then click here to see how it is done.

I/D #3: Unit Q- Pythagorean Theorem

Inquiry Activity Summary: 
Where does sin^2x+cos^2x=1 come from?

The Pythagorean theorem is derived to become a Pythagorean identity. From the unit circle, the Pythagorean theorem uses "x", "y", and "r" which would become: x^2+y^2=r^2. With this we can perform an operation which allows the equation equal to 1. The operation is to just simply divide r^2 from both sides of the equation which in turn creates (x/r)^2+ (y/r)^2= 1. This then becomes an identity, proven facts and formulas that are always true. From the unit circle we see that cosine equals x/r and sine equals y/r, with these two we can just substitute them into the equation which will then give us the Pythagorean Identity sin^2x+cos^2x=1.

Show and explain how to derive the two remaining Pythagorean Identities from sin^2x+cos^2x=1.

Please look at the pictures below, they already have the descriptions on how I got other two remaining Pythagorean Identities.

Inquiry Activity Reflection:

The connections that I see between Units N, O, P, and Q so far are that they all relate back to the Unit circle. The reason why I say this is because of the fact that when we derive triangles, Heron's Theory, and any of the other equations that we have learned prior to this would reference back to the Unit circle for the legs and hypotenuse which will help us to derive the triangle or theory.

If I had to describe trigonometry in three words, they would be complicated, interesting, and enjoyable. It's complicated because we learn not only the equations and theories given to us but we also learn how it was derived and how it is connected with the real world. It is interesting because prior to learning these mathematical equations and theories you don't really question the math that is going on around you and you especially don't think about how these formulas were derived, so it makes it interesting to see all the math that is around you everyday. And finally it is enjoyable because when you finally understand how to do the problems and understand how you are connected to it, you start to enjoy answering the problem and you begin to see that math isn't as bad as many may think it is.

WPP 13 & 14: Unit P Concepts 6-7

This WPP 13-14 was made in collaboration with Genesis R.. Please visit the other awesome posts on her blog here.

Hershey has stopped at a stoplight and noticed that his best friend, Marlene, is due west of him at the next stoplight, 30 feet away. Both are going to Hershey's Bakery. Hershey walks N 30* W to get there while Marlene goes N 72* E to get there. What is both of their distances to walk over to Hershey's Bakery?

After having a nice, long conversation with Hershey, they decided to see each other again the next day. They both leave the bakery at the same time. Marlene, in hurry to get to her cousin's Quinceanera, is headed at a bearing of 315* and is traveling 50 MPH. Hershey on the other hand goes home at 30 MPH at a bearing of 078*. How far apart are they after two hours?

BQ #1- Unit P: Concepts 1&4: Law of Sines AAS or ASA and Area of an Oblique Triangle

i-Law of Sines:
Why do we need it?
The law of sines is of importance because it helps us to find non-right triangles that are commonly seen in the real world. With this we are able to find any unknown angle or side if we have already found or were given two angles and one side as well we could have been given two sides and one angle.
How is it derived from what we already know?

http://i1.ytimg.com/vi/Bj7h6OMBvqk/hqdefault.jpg

 When given an unknown triangle with some given information on the side and two angles, when deriving it we can just form a line straight down from the middle to give us two 90 degree triangles. With this we can use Sine and it will  be something as below where we get a ratio. However since we want Sine by itself we multiply through to receive the final answer.

http://www.lhs.loganschools.org/~rweeks/trig/law_of_sines.jpg

iv-Area Formulas:
How is the "area of an oblique" triangle derived?
 When given a triangle with some of the given angles and side we just cut the triangle in half for we can receive two 90 degree triangles. With this we then use SOHCAHTOA to get a ratio, with this we can substitute it in for the height of the area formula we are used to, for we can use to solve the area of the triangle.

https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgRUfaYjkTy5hlsAuerPsDTfulo_zx2qECBMGIWGwX-EcYy4zuaMlV3LC1XqmMsvMpN1kXNTXUSw9HJScLKdDdZdydgqvLghasCFxtONLYiSbtPDbOBMUe9xWWI1TqvDtxuW0-MR7RxxZY/s400/hi.bmp

How does it relate to the area formula that you are familiar with?
This relates to the area formula (a=1/2bh) that we are familiar with because we solve with this formula however we substitute "h" with 1/2abSinC or any of the others.

References:
http://www.lhs.loganschools.org/~rweeks/trig/law_of_sines.jpg
http://facstaff.gpc.edu/~ahendric/Math1113/sec6_1notes/images/pic010.jpg
http://i1.ytimg.com/vi/Bj7h6OMBvqk/hqdefault.jpg
https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgRUfaYjkTy5hlsAuerPsDTfulo_zx2qECBMGIWGwX-EcYy4zuaMlV3LC1XqmMsvMpN1kXNTXUSw9HJScLKdDdZdydgqvLghasCFxtONLYiSbtPDbOBMUe9xWWI1TqvDtxuW0-MR7RxxZY/s400/hi.bmp

WPP #12: Unit O: Concept 10- Solving angle of evelvation and depression word problems

Create your own Playlist on LessonPaths!

I/D #2: Unit O- How can we derive the patterns for our special right triangles?

1-"Something that I never noticed before about special right triangles is ..." that when you use other numbers other than the ones given you get a similar answer as you did with the numbers given to you.
2-"Being able to derive these patterns myself aids in my learning because ..." it helps to know how you got these equation for the special right triangles and it helps you learn what you are doing.

I/D #1 Unit N: Concepts 7-9: How do you SRT and UC relate?

Inquiry Activity Summary:
Please watch the videos below because they will help you in understanding from where we get our points for the unit circle and they will show you how the special right triangles relate to the unit circle:

This video helps you to derive from the unit circle in how it is a thirty degree angle and is one of the often used angle and it helps to know how the point for this degree on the unit circle came from. When the triangle is drawn in a different quadrant not only does the degree change but the x or y values can change into a negative.

This video helps to derive from the unit circle in how it is the forty-five degree angle and it is able to help us know how we got the point for this degree on the unit circle. When the triangle is drawn in a different quadrant the x or y can become a negative or the both can become a negative.

This video helps to derive from the unit circle in how it is able to help us learn in how we got the points for this degree. When the triangle is in another quadrant both the x and y can become negative but the point given to us will still be the same.

Inquiry Activity Reflection:
 The coolest thing I learned from this activity was how we actually got the points and all the math that actually happens behind the unit circle.
 This activity helped me on this unit because it made it a lot easier for me to understand and memorize the unit circle.
 Something I never realized before about the special right triangles and the unit circle is the fact they related to one another and that they make it a lot more easier to figure out what is the points of these angles.

RWA #1: Unit M Concepts 4-6: Conic Sections in Real Life

Parabolas:
1-"The set of all points that are equidistant from a point that is known as the focus and a line known as the directrix." (Mrs.Kirch's LessonPaths Playlist Unit M Concept 4a)
2- The equation for a parabola is (x-h)^2=4p(y-k) or (y-k)^2=4p(x-h), with this we are able to receive pieces of information and will help to graph out the needed information.

http://www.mathwords.com/p/p_assets/parabola%20features%20focus%20directrix%20vertex%20axis.gif

     Some of the key features for the graphing of this conic section is the fact of seeing whether it goes up, down, left or right. Well to figure this out you must look to see which goes first/is squared and by this I mean the "x" and "y" in the equation that was given in the first sentence above the picture. With this information you will be able to learn whether it goes up/down or left/right as well will you be able to identify the center/vertex is by using the "h" and "k" that is given in the equation. However it will need "p" for you can further know if it is going to the right or down, "p" is the space between the focus and the vertex as well as the distance between the vertex and directrix. With this in mind, "p" has a huge impact on the hyperbola for it can show us whether the graph will be thin or wide but it also shows us the slope for the graph.
      There is also the directrix, which is given or you must find, and this helps to show you were your parabola must go over or next to. With the directrix you get the general idea of how the graph should look like at the end. There is also an axis of symmetry that goes through the focus and vertex and helps us to see in which direction the parabola should go into. However if still confused here is a video that may help you to further understand hyperbolas.

3- What it can be in the real world (example):

http://i00.i.aliimg.com/img/pb/179/937/366/366937179_304.jpg

      A real world application of a hyperbola may be a jet of water, for better definition I mean the formation of the water of a fountain. What I mean is that when the water is going upward gravity is still pulling down making the water curve making it look like a parabola.
      If this was graphed out it would have a directrix right above the curving point, in which we can consider as the vertex, and a focus that will show us the approximation of how wide the water will be when falling back into the fountain. If you want to know more or just want to see more of what parabolas are in real life go here: http://www3.ul.ie/~rynnet/swconics/UP.htm

 4- Work cited:
"Applications of Hyperbolas." Applications of Hyperbolas. N.p., n.d. Web. 09 Feb. 2014.
  "Equation of a Parabola (conic Section)." YouTube. YouTube, 13 Mar. 2013. Web. 09 Feb. 2014
 "This Learning Playlist Is Empty." LessonPaths. N.p., n.d. Web. 11 Feb. 2014.
 http://i00.i.aliimg.com/img/pb/179/937/366/366937179_304.jpg
http://www.mathwords.com/p/p_assets/parabola%20features%20focus%20directrix%20vertex%20axis.gif

WPP #10: Unit L Concepts 9-14: Probability, Independent, Dependent, Mutually and Non-mutally Exclusive

Create your own Playlist on LessonPaths!